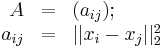Euclidean distance matrix

In mathematics, a Euclidean distance matrix is an n×n matrix representing the spacing of a set of n points in Euclidean space. If A is a Euclidean distance matrix and the points are defined on m-dimensional space, then the elements of A are given by

$\begin{array}{rll} A & = & (a_{ij}); \\ a_{ij} & = & ||x_i - x_j||_2^2 \end{array}$

where ||.||₂ denotes the 2-norm on R^m.

Properties

Simply put, the element a_ij describes the square of the distance between the i ^th and j ^th points in the set. By the properties of the 2-norm (or indeed, Euclidean distance in general), the matrix A has the following properties.

All elements on the diagonal of A are zero (i.e. is it a hollow matrix).
The trace of A is zero (by the above property).
A is symmetric (i.e. a_ij = a_ji).
a_ij^1/2 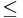$\le$ a_ik^1/2 + a_kj^1/2 (by the triangle inequality)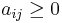
$a_{ij}\ge 0$
The number of unique (distinct) non-zero values within an N-by-N Euclidean distance matrix is bounded (above) by [N*(N-1)] / 2 due to the matrix being symmetric and hollow.

References

James E. Gentle (2007). Matrix Algebra: Theory, Computations, and Applications in Statistics. Springer-Verlag. p. 299. ISBN 0387708723.

Euclidean distance matrix

Properties

See also

References